Items added to your cart
Size:

Curiosity is one of the most powerful forces that drives human learning and discovery. From the moment we are born, we are wired to wonder, ask questions, and seek out...
Curiosity is one of the most powerful forces that drives human learning and discovery. From the moment we are born, we are wired to wonder, ask questions, and seek out...
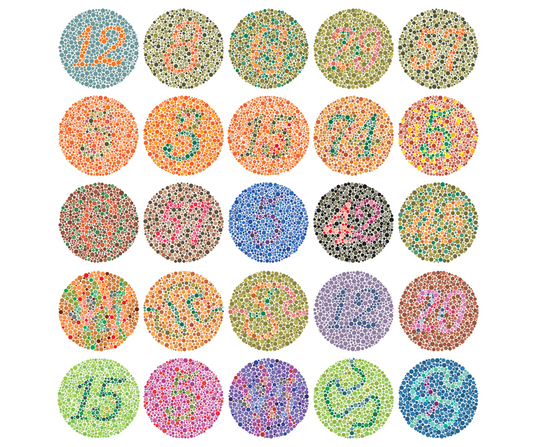
Have you ever shown someone a bright red shirt only for them to call it brown? Or maybe someone you know can’t spot the difference between green and yellow traffic...
Have you ever shown someone a bright red shirt only for them to call it brown? Or maybe someone you know can’t spot the difference between green and yellow traffic...

Imagine savoring a slice of lemon and simultaneously seeing a burst of yellow light. For some individuals, this is not imagination but reality. This phenomenon is known as synesthesia, a...
Imagine savoring a slice of lemon and simultaneously seeing a burst of yellow light. For some individuals, this is not imagination but reality. This phenomenon is known as synesthesia, a...

When it comes to learning, there’s a big difference between simply reading about something and actually doing it. That’s the power of hands-on learning — a method that turns passive...
When it comes to learning, there’s a big difference between simply reading about something and actually doing it. That’s the power of hands-on learning — a method that turns passive...

When we look at images from space, we are dazzled by swirls of purple, blue, orange, and green. From the breathtaking hues of nebulae to the glowing surface of distant...
When we look at images from space, we are dazzled by swirls of purple, blue, orange, and green. From the breathtaking hues of nebulae to the glowing surface of distant...
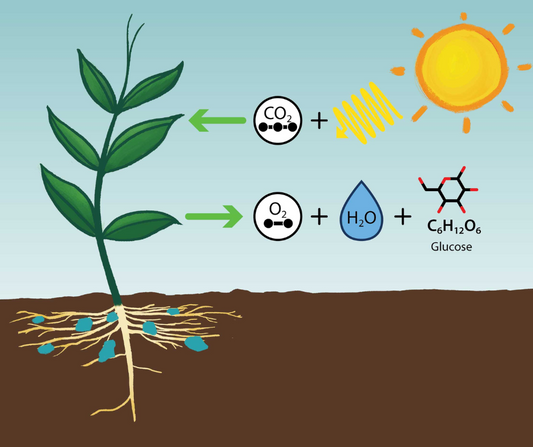
Plants are remarkable organisms that play a crucial role in sustaining life on our planet. Unlike animals, plants have the unique ability to create their own food using just sunlight,...
Plants are remarkable organisms that play a crucial role in sustaining life on our planet. Unlike animals, plants have the unique ability to create their own food using just sunlight,...